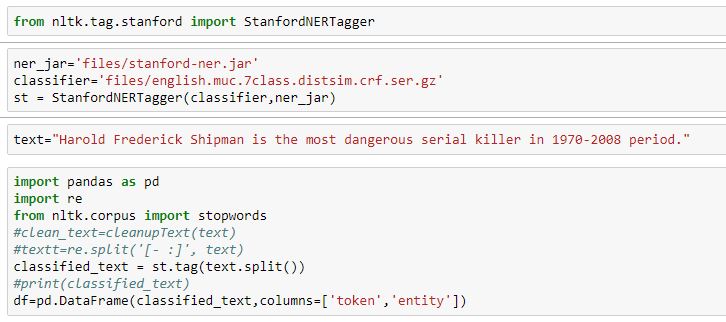
Bayesien classifier

Bayesien classifier

   September 18, 2017       Emna Amor

---

The simplest solutions are the most powerful, and Naive Bayes is a good example. Despite the great advances in machine learning in recent years, it has proven to be not only simple but also fast, accurate and reliable. It has been successfully used with several fins, but it works very well with natural language processing problems.

Naive Bayes is a family of probabilistic algorithms that take advantage of probability theory and Bayes' theorem to predict the category of a sample. They are probabilistic, which means they calculate the probability of each category for a given sample, and then output the category with the highest probability. The way they obtain these probabilities is by using the Bayes theorem, which describes the probability of a feature, depending on prior knowledge of the conditions that could be related to this feature

We will work with an algorithm called Multinomial Naive Bayes. So at the end we will know how this method works, but also why it works. Then we will be able to do some advanced techniques that can make Naive Bayes competitive with more complex machine learning algorithms, such as SVM and neural networks..

example:

Text	Category
“Barack Obama is the president of the U.S”	Politics
“Football is my favorite game”	Sports
“federer wimbledon is the best Tennis Player ”	Sports
“i need to contact my bank to get a loan”	Financial world
“Trump is the most stupid president”	Politics

Now, which category does the sentence "Barack Obama is the president of the U.S" belong to?

Because Naive Bayes classifier is probabilistic, we want to calculate the probability that the sentence "Barack Obama is the president of the U.S" is Politics, and the probability that it is in other categories. Then we take the largest one. Mathematically, what we want is P (Politics | Barack Obama is the president of the U.S) which means the probability that the category of a sentence is Politics given that the sentence is "Barack Obama is the president of the U.S".

Great, but how do we calculate those probabilities? Let's see!!

Feature-Extraction

The first thing we need to do when creating a machine learning model is to decide what to use as features. It is well known that reducing the number of input variables through dimensionality reduction techniques such as feature extraction is desirable. Features are expected to contain the relevant information from the input data, so that the desired task can be performed by using this reduced representation instead of the complete initial data. To better understand this approach,  let's say that we are training a model for "health and medicine" category. A person's height or weight is important for us but the person name, eye color or skin color is not important for the model, so we exclude those unuseful features. 

But, in this case, we don’t even have numeric features. We just have text. We need to somehow convert this text into numbers that we can do calculations on which is known by words to frequencies.

From Words to Frequencies

we ignore word order and sentence construction, treating every document as a set of the words it contains. Our features will be the counts of each of these words. Even though it may seem too simplistic an approach, it works surprisingly well. We call vectorization the general process of turning a collection of text documents into numerical feature vectors. This specific strategy (tokenization, counting and normalization) is called the Bag of Words or “Bag of n-grams” representation. Documents are described by word occurrences while completely ignoring the relative position information of the words in the document.

Bayes Theorem

Now we need to transform the probability we want to calculate into something that can be calculated using word frequencies. That's why we will use some basic properties of probability and bayes theorem. To work with Bayes theorem, you need to know about conditional probability.

Conditional probability can be thought of as looking at the probability of one event occurring with some relationship to one or more other events. For example:

• Event A is that it is snowing outside, and it has a 0.3 (30%) chance of snowing today.
• Event B is that you will need to go outside, and that has a probability of 0.5 (50%).

A conditional probability would look at these two events in relationship with one another, such as the probability that it is both snowing and you will need to go outside.

The formula for conditional probability is:

P(B|A) = P(A and B) / P(A)

which can also be rewritten as:

P(B|A) = P(A∩B) / P(A) 

or  P(A∩B)=P(A|B) .P(B)

P(B|A) = P(A|B) .P(B) / P(A)

In our case, using the conditional probability theorem, we have P(Politics | Barack Obama is the president of the U.S)=P(Barack Obama is the president of the U.S | Politics ) . P(Politics) / P(Barack Obama is the president of the U.S)

Since for our classifier we’re just trying to find out which category has a bigger probability, we can discard the divisor for all probability calculations P(Politics | Barack Obama is the president of the U.S), P(Sports | Barack Obama is the president of the U.S), P(Financial world | Barack Obama is the president of the U.S) .....

We will just count how many times the sentence “Barack Obama is the president of the U.S” appears in the Politics category, divide it by the total, and obtain P(Barack Obama is the president of the U.S | Politics).

But this way, We could have a problem: “Barack Obama is the president of the U.S” could not appear in our training set, so the probability will be zero. Unless every sentence that we want to classify appears in our training set, the model would not be useful.

Naive Bayes
Here we can talk about Naive Bayes. Being naive will help us to get a better model to classify our sentence in the correct category. We suppose that every word in a sentence is independent from the others. That means that we will no longer look for the probability of the entire sentence, but we yill search the probability of individual words.
So "Barack Obama is the president of the U.S" is the same as "the president of the U.S is Barack Obama " as well as "Obama Barack is the president of the U.S" ..
Therefore,  P(Barack Obama is the president of the U.S)= P(Barack)*P(Obama)*P(is)*P(the)*P(president)*P(of)*P(the)*P(U.S)

This hypothesis is very strong and super useful. This is why this model works well with small data set or data that can be mislabeled. The next step is exactly what we had before:
P(Barack Obama is the president of the U.S | Politics )= P(Barack | Politics)*P(Obama | Politics)*P( is | Politics )*P( the | Politics )*P( president | Politics )*P( of | Politics )*P( the | Politics )*P( U.S | Politics )

Now all of these individual words show up several times in our training set, and we can calculate them! 
The final step is just to calculate every probability (for each category) and see which one turns out to be larger.

Read More

Data Visualization using Lda and T-SNE

Data Visualization using Lda and T-SNE

   August 05, 2017       Emna Amor

---

LDA (linear discriminant analysis)

Linear Discriminant Analysis (LDA) is most commonly used as dimensionality reduction technique in the pre-processing step for pattern-classification and machine learning applications. The goal is to project a dataset onto a lower-dimensional space with good class-separability in order avoid overfitting (“curse of dimensionality”) and also reduce computational costs.

The SNE

The Stochastic Neighbor Embedding (SNE) method consists of converting the large-dimensional Euclidean distances between the data points into conditional probabilities which have the similarities.
For the homologues yi and yj of the data points xi and xi, it is possible to calculate the similar conditional probability denoted Qj / i. The variance is fixed at 1/21/2 



Since we are interested in matched similarities, on met Qj / i = 0. If the points yi and yj correctly model the similarity between the data points, the conditional probabilities are equal. On the basis of this observation, the SNE aims to find a small dimensional presentation that minimizes the offset between Pj / i and Qj / i. But the different types of errors in the corresponding distances are not equally weighted. In particular, the cost remains important for the use of widely separated points.

The T-SNE

The SNE as presented by Hinton and Roweis has good visualizations but hampered by a function of cost difficult to optimize.
The t-SNE is a new technique that aims to alleviate the problem by using a new version of the cost function of symmetric SNE with simpler gradients, and also using the student rather than the Gaussian for computation Of the similarity between two points in small space.


Today we will work with a known dataset called 20_newsgroups.
and we had this lda and T-SNE representation.

LDA Visualization 

T-SNE Visualization

Here you can find the full notebook.

Read More

NLP Processing using NLTK Stanford core nlp

NLP Processing using NLTK Stanford core nlp

   July 27, 2017       Emna Amor

---

Can computers understand humans?

NLP is a very important branch of Machine Learning and therefore of artificial intelligence. The NLP is the ability of a program to understand human language.

Let's take a few practical examples that are used every day to better understand:

• Spam: all mailboxes use an anti-spam filter and it works with Bayesian filtering in reference to the Bayes theorem which is a statistical technique for detecting spam. These filters will "understand" the text and find out if there are correlations of words that indicate spam.

• Google Translation: you probably have all used this system and their technology uses many algorithms including NLP. Here, the challenge is not to translate the word, but to keep the meaning of a sentence in another language.

• The Siri software created by Apple or Google Assistant uses NLP to translate transcribed text into analyzed text in order to give you an answer adapted to your request.

Today we will make some NLP processing, using NLTK Stanford core nlp.

We need for that jupyter notebook and python3.

You can find the full notebook HERE

POS-Tag

The process of classifying words into their parts of speech and labeling them accordingly is known as part-of-speech tagging, POS-tagging, or simply tagging. Parts of speech are also known as word classes or lexical categories. The collection of tags used for a particular task is known as a tagset.

 

Parsing

A natural language parser is a program that works out the grammatical structure of sentences, for instance, which groups of words go together (as "phrases") and which words are the subject or object of a verb.

NER

Named Entity Recognition (NER) labels sequences of words in a text which are the names of things, such as person and company names, or gene and protein names

Here are the results

We will try to remove the other things.

Coref-Resolution

Coreference resolution is the task of finding all expressions that refer to the same entity in a text. It is an important step for a lot of higher level NLP tasks that involve natural language understanding such as document summarization, question answering, and information extraction.

I will use core nlp server for coreference resolution 

You can run the server using this command:

java -mx4g -cp "*" edu.stanford.nlp.pipeline.StanfordCoreNLPServer

You can use the server for parsing , part of speech tagging or any other tool of stanford core nlp.

Read More

Arabic named entity recognition

Arabic named entity recognition

   July 27, 2017       Emna Amor

---

Information Extraction 

An important approach to text mining involves the use of natural-language information extraction. Information extraction (IE) distills structured data or knowledge from unstructured text by identifying references to named entities and relations between those entities.

Arabic named entity recognition

 It's easy to make named entity recognition using Stanford core nlp, or Spacy or NLTK, ect.., but having good results for arabic language is not that easy.

Today we will use an arabic corpus called ANERCorp (you can download it using this link). It is a manually annotated corpus in Arabic which is created to be used in Arabic NER tasks. It consists of two parts; training and testing. It has been annotated by one person in order to guarantee the coherence of the annotation.

Here is the Full noteook

Let's load our files

If we visualize our data frame, we can notice that the last column is not necessary, so, we will drop it and we will rename our columns.

this is how our data frame become.

       

First of all, let's understand the meaning of the entities. We can say that we have 4 entities in general, but here, we will find 8.

How?

B-PERS: Beginning of Person Name

I-PERS: Inside of Person Name

B-LOC: Beginning of Location Name

I-LOC: Inside of Location Name

B-ORG: Beginning of Organization Name

I-ORG: Inside of Organization Name

B-MISC: Beginning of Miscellaneous Word

I-MISC: Inside of Miscellaneous Word

Those are our 8 entities, each with a beginning and inside. The "O" designs the words that are not named entities, so O is referred to Object.

Now, we will split the data to test and train data (20% and 80%), and we will put the data and the labels into arrays.

Then, we will convert data to a matrix of features using CountVectorizer and TFIDF.

I will use Linear Svm to train the model ( you can try any other classifier)

and now, we can make a test, 

ألمانيا  is Germany
so our program shows that Germany is a location.

Read More

Text Classification

Text Classification

   July 27, 2017       Emna Amor

---

         Today we're going to learn a great machine learning technique called document classification. We will use different classifiers such as Naive Bayes, SVM and KNN.

Introduction to document classification

Document classification is an example of Machine Learning (ML) in the form of Natural Language Processing (NLP). By classifying text, we are aiming to assign one or more classes or categories to a document, making it easier to manage and sort. This is especially useful for publishers, news sites, blogs or anyone who deals with a lot of content. 

When you will search on the net for document classification, you will find that there are lots of applications of text classification in the commercial world just like email spam filtering is perhaps now the most ubiquitous

Today we will work with ag_news Dataset (link to download).Put another way: "given a piece of text, determine if it belongs to Sports, science and tech, world or Business category".

we will use:

           -Python 3

           -Jupyter notebook

Here you can find the full notebook. 

Load Data

When opening the CSV file, we can see 3 columns which are [category, title, text]. We will be interested in 2 columns which are category and text.

and now we can see our data frame.

then we will replace Nan Values if they exists with space.

I am going to delete title, if you don't want to delete it, you can join title and text to one field like this: 

we added a new column called full_text and we will delete the others to keep the memory.

For my case, i just deleted titles.

Now we will enumerate our class names

and also, we will change our category column, from numbers to names.

 Now everything is ready and we need to begin. First of all we will clean our data and we will stem them. The goal of Stemming is to "normalize" words to their common base form, which is useful for many text-processing apllications especially in our case "document classification".

So, we have this function which keep only-alphanumeric characters and replaces all white space with a single space.

Now, we will convert data frame series to list

Now, we will convert our text to a matrix of features, therefore, we will use scikit-learn countVectorizer and tfidTransformer.

Now we will build our models! 

Let's begin with Naive Bayes ( I will try Bernoulli Naive Bayes and Multinomial Naive Bayes)

But before, let's make a confusion matrix function to use it with all the classifiers.

Naive Bayes

Bernoulli Naive Bayes

Let's plot it confusion matrix (we forgot to import numpy before the confusion matrix function, just add import numpy as np)

Multinomial Naive Bayes

SVM

Linear SVM

 

Non-Linear SVM

KNN

Never hesitate to ask questions if you have :) 

Read More